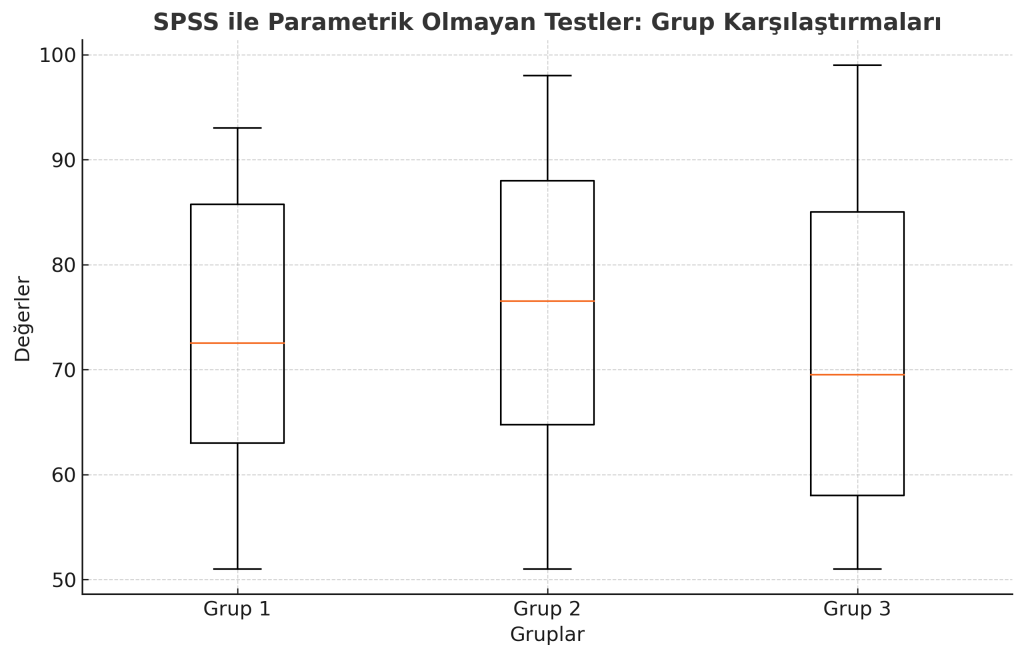
SPSS ile veri analizi yaparken, bazı durumlarda parametrik testler (t, Z ve F testleri) kullanılamaz. Bunun temel sebebi, parametrik testlerin ana kütle dağılımının normal olması gerekliliğidir. Eğer veri normal dağılım göstermiyorsa, dağılımdan bağımsız olan parametrik olmayan testler uygulanır. Bu testler, sürekli dağılım gösteren veriler için uygundur ve örneklem büyüklüğünden bağımsız olarak kullanılabilir.
Parametrik Olmayan Testler Nelerdir?
Parametrik olmayan testler, üç ana gruba ayrılır:
- Tek Örneklem Testleri
- İki Örneklem Testleri
- K-Örneklem Testleri
Tek Örneklem Testleri
Tek örneklem testleri, tek bir veri grubunun belirli bir dağılıma veya teorik bir değere uygun olup olmadığını test etmek için kullanılır.
- Binominal Test: Evet-Hayır, olumlu-olumsuz gibi iki yönlü olayları analiz eder. Veriler simgesel olarak 1 ve 0 şeklinde gösterilir.
- Ki-Kare Uygunluk Testi: Elde edilen frekans tablolarının teorik değerlerle ne kadar uyumlu olduğunu test eder.
- Kolmogorov-Smirnov Uygunluk Testi: Rastgele seçilen bir örneklemin belirli bir dağılıma sahip olup olmadığını değerlendirir.
- Diziler Testi (Runs): Örneklem içindeki değerlerin sırasının rastgele olup olmadığını kontrol eder.
İki Örneklem Testleri
İki örneklem testleri, iki farklı veri grubunun birbirine benzer olup olmadığını belirlemek için kullanılır.
1. Eşleştirilmiş İki Örneklem Testleri
- İşaret Testi: İki bağımlı grup arasında medyan farkı olup olmadığını test eder.
- Wilcoxon İşaret Sıralaması Testi: Bağımlı iki grup arasında fark olup olmadığını belirlemek için sıralı verileri kullanır.
- McNemar Testi: Kategorik verilerde öncesi-sonrası analizleri için uygundur.
2. Bağımsız İki Örneklem Testleri
- Kolmogorov-Smirnov Z Testi: İki bağımsız örneklemin aynı dağılımdan gelip gelmediğini test eder.
- Mann-Whitney U Testi: İki bağımsız grubun medyanlarının karşılaştırılmasını sağlar.
K-Örneklem Testleri
K-örneklem testleri, birden fazla grubun karşılaştırılmasını sağlar. Bu testler eşleştirilmiş K-örneklem testleri ve bağımsız K-örneklem testleri olarak ikiye ayrılır.
1. Eşleştirilmiş K-Örneklem Testleri
- Cochran Q Testi: Üç veya daha fazla eşleştirilmiş grup için kategorik verilerde bağımlılık olup olmadığını test eder.
- Friedman Testi: Üç veya daha fazla bağımlı grubun medyanlarını karşılaştırmak için kullanılır.
2. Bağımsız K-Örneklem Testleri
- Kruskal-Wallis H Testi: Üç veya daha fazla bağımsız grup arasında istatistiksel olarak anlamlı fark olup olmadığını belirler.
Parametrik Olmayan Testlerin Uygulama Alanları
SPSS ile veri analizi yaparken parametrik olmayan testler, şu durumlarda kullanılır:
- Veri normal dağılım göstermediğinde.
- Örneklem büyüklüğü küçük olduğunda.
- Veriler sıralı veya kategorik olduğunda.
- Aykırı değerlerin etkisini azaltmak gerektiğinde.
Sıkça Sorulan Sorular (SSS)
SPSS ile parametrik olmayan testler, dağılımdan bağımsız analizler yapmak isteyen araştırmacılar için güçlü bir araçtır. Doğru test seçimiyle verilerinizden en iyi içgörüleri elde etmek için Veri Analiz Merkezi ile iletişime geçin!



